五米高考> >高考复习 >高中数学 >

湖南省长沙市长沙县高一（上）期末数学试卷

时间： 高中数学

2021长沙县一中高一（上）期末数学卷


一．选择题：本大题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。1．已知集合P＝{2，4，6，8}，则集合P的真子集的个数是（　　）
A、4 B、14 C、15 D、16

2．命题p：7?x0∈R，x02＋2x0＋2≤0，则￢p为（　　）
A、?x0∈R，x02＋2x0＋2＞0
B、?x0?R，x02＋2x0＋2＞0
C、?x∈R，x2＋2x＋2＞0
D、?x∈R，x2＋2x＋2≤0

3．如果a＜0，b＞0，那么，下列不等式中正确的是（　　）
A、
1
a
＜
1
b
B、
? ?a
＜
? b
C、a2＜b2 D、|a|＞|b|

4．下列每组函数是同一函数的是（　　）
A、f（x）＝x0与f（x）＝1
B、f（x）＝
? x2
?1与f（x）＝|x|?1
C、f（x）＝
x2?4
x＋2
与f（x）＝x?2
D、f（x）＝
? (x?1)(x?2)
与f（x）＝
? x?1
? x?2

5．下列函数在[1，4]上最大值为3的是（　　）
A、y＝
1
x
＋2 		B、y＝3x?2
C、y＝x2 D、y＝3x

6．将函数y＝cosx?1的图象向左平移
π
2
个单位长度，再向上平移1个单位长度，得到的图象对应的函数解析式为f（x）＝（　　）
A、sinx B、?sinx
C、cosx D、?cosx
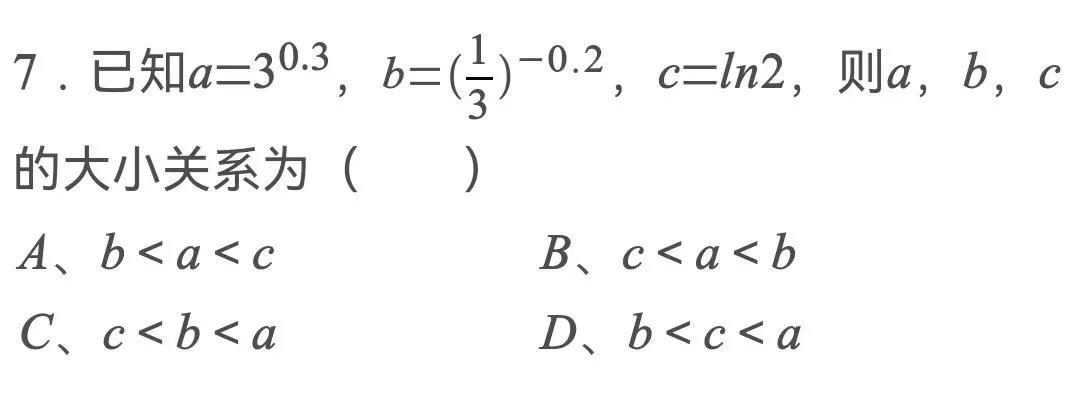?8．已知e是自然对数的底数，函数f（x）＝ex＋x?2的零点为a，函数g（x）＝lnx＋x?2的零点为b，则下列不等式中成立的是（　　）
A、a＜1＜b B、a＜b＜1
C、1＜a＜b D、b＜1＜a

二．选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得3分．9．已知M＝{x∈R|x≥3}，a＝π，有下列四个式子：（1）a∈M；（2）a?M；（3）{a}?M；（4）{a}∩M＝π，其中正确的序号是（　　）
A、（1） B、（2）
C、（3） D、（4）

10．已知实系数一元二次方程ax2＋bx＋c＝0（a≠0），下列结论正确的是（　　）
A、Δ＝b2?4ac≥0是这个方程有实根的充要条件
B、Δ＝b2?4ac＝0是这个方程有实根的充分条件
C、Δ＝b2?4ac＞0是这个方程有实根的必要条件
D、Δ＝b2?4ac＜0是这个方程没有实根的充要条件
11．下列选项中，与sin
5
6
π 的值相等的是（　　）
A、cos（?
π
3
）
B、cos18°cos42°?sin18°sin42°
C、2sin15°sin75°
D、
tan30°＋tan15°
1?tan30°tan15°

?

三．填空题：本大题共4小题，每小题5分，共20分。13．不等式x2?2x＋3＜0的解集是 ．
14．已知（a2＋a＋2）x＞（a2＋a＋2）1?x，则x的取值范围是 ．15．已知函数f（x）是R上的奇函数，且f（x＋2）＝?f（x），当x∈（0，2）时，f（x）＝x2，则f（7）＝　．16．国际油价在某一时间内呈现出正弦波动规律：P＝Asin（ωπt＋
π
4
）＋60（美元）[t（天），A＞0，ω＞0]，现采集到下列信息：最高油价80美元，当t＝150（天）时达到最低油价，则ω的最小值＝　．
四．解答题：本大题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤。?
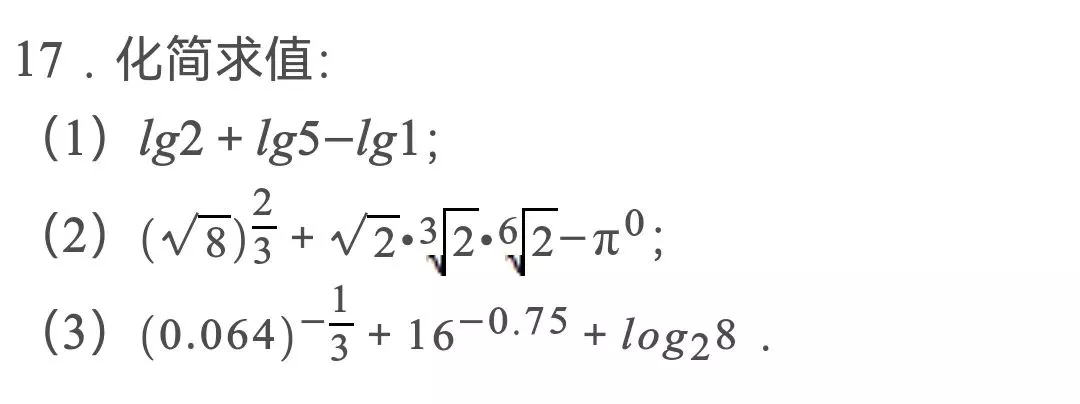18．已知集合A＝{x|y＝
? (2＋x)(4?x)
}，B＝{x|?1＜x＜m＋1}．
（1）求集合A；
（2）若m＝4，求A∪（?RB），（?RA）∩B；
（3）若A∪B＝A，求实数m的取值范围．
19．甲、乙两地相距1000千米，某货车从甲地匀速行驶到乙地，速度为v千米/小时（不得超过120千米/小时）．已知该货车每小时的运输成本m（以元为单位）由可变部分y1和固定部分y2组成：可变部分与速度v（单位：km/h）的关系是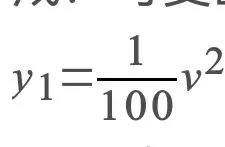?固定部分y2为81元．
（1）根据题意可得，货车每小时的运输成本m＝　，全程行驶的时间为t＝　；
（2）求该货车全程的运输总成本与速度v的函数解析式；
（3）为了使全程的运输总成本最小，该货车应以多大的速度行驶？

20.?


21．某上市股票在30天内每股的交易价格P（元）与时间t（天）组成有序数对（t，P），点（t，P）落在如图所示的两条线段上．该股票在30天内（包括30天）的日交易量M（万股）与时间t（天）的部分数据如表所示：
第t天 6 13 20 27
M（万股） 34 27 20 13
（1）根据提供的图象，写出该股票每股交易价格P（元）与时间t（天）所满足的函数关系式P＝　；
（2）根据表中数据，写出日交易量M（万股）与时间t（天）的一次函数关系式：M＝　；
（3）用y（万元）表示该股票日交易额，写出y关于t的函数关系式，并求在这30天内第几天日交易额最大，最大值为多少？
22．已知函数f（x）＝
x?m
nx2＋1
是定义在[?1，1]上的奇函数，且f（1）＝
1
2
．
（1）求m，n的值；
（2）判断f（x）在[?1，1]上的单调性，并用定义证明；
（3）设g（x）＝kx＋5?2k，若对任意的x1∈[?1，1]，总存在x2∈[0，1]，使得f（x1）≤g（x2）成立，求实数k的取值范围．



??唐老师13875977169～成绩提升看得见??





2021?2022学年湖南师大附中高一（上）第一次大练习数学试卷（12月份）一、单选题：本大题共8个小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若a＜b＜0，则下列不等式正确的是（　　）
A、
1
a
＜
1
b
B、ab＞a2
C、|a|＜|b| D、a2＞b2

2．下列各组函数中，表示同一函数的是（　　）?

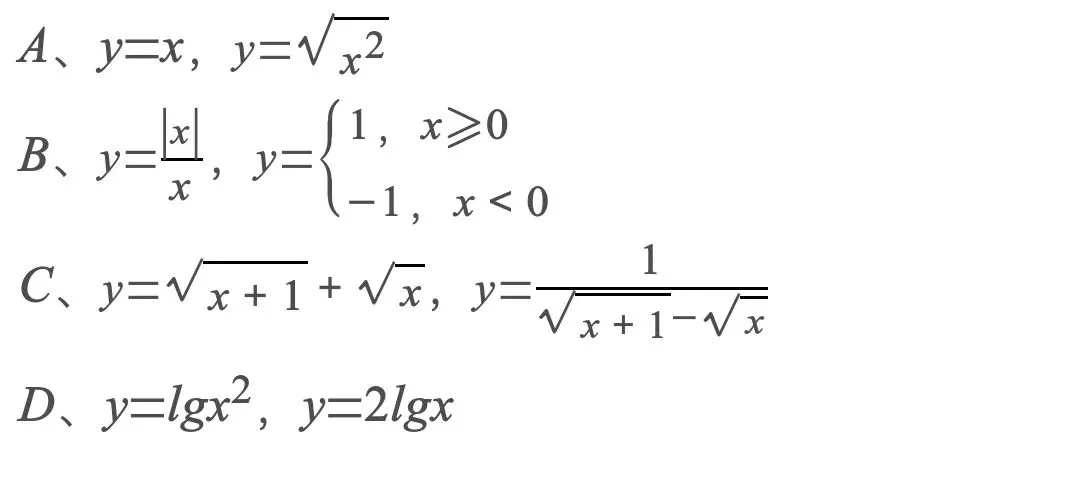3．已知a＝log3π，b＝log0.72，c＝0.90.9，则a，b，c的大小关系为（　　）
A、a＞b＞c B、c＞a＞b
C、a＞c＞b D、b＞a＞c

4．命题“?x∈[1，2]，3x2?a≥0”为真命题的一个充分不必要条件是（　　）
A、a≤2 B、a≥2
C、a≤3 D、a≤4

5．已知a＞1，函数y＝a?x与y＝loga（?x）的图象只可能是（　　）
A、 B、
C、 D、
6．英国经济学家马尔萨斯在1798年提出了自然状态下的人口增长模型为：y＝y0ert，其中t表示经过的时间（单位：年），y0表示t＝0时的人口数，r表示人口的年平均增长率．若某国的人口年平均增长率为2%，该国2020年底人口数量为m，则预计到（　　）年底，该国的人口翻一番（即2倍）．（注：ln2≈0.7）
A、2050 B、2055
C、2060 D、2065

7．已知两个正实数a，b满足a?b＞lnb?lna，则下列不等式恒成立的是（　　）
A、lg（a?b）＞0 B、ln（a?b＋e）＞1
C、e（b?a）＞1 D、e（a?b）＞e

8．已知函数f（x）对?x1，x2∈R，总有（x1?x2）[f（x1）?f（x2）]＞0，若不等式f（3a?x）≤f（x＋a2）对?x∈（a?1，a）恒成立，则实数a的取值范围是（　　）
A、[?1，2]
B、[0，1]
C、（?∞，0]∪[1，＋∞）
D、（?∞，?1]∪[2，＋∞）
二、多选题：本大题共4个小题，每小题5分，满分20分．在每小题给出的选项中，有多项是符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得2分．9．已知角α的顶点与原点重合，始边与x轴的非负半轴重合，终边经过点P（m，1?m），若m＞0，则下列各式一定为正值的是（　　）
A、sinα B、cosα
C、sinα?cosα D、sinα＋cosα


?

11．已知函数f（x）＝lnx＋ln（2?x），则（　　）
A、f（x）在（0，1）上单调递增
B、f（x）在（1，2）上单调递增
C、y＝f（x）的图象关于直线x＝1对称
D、y＝f（x）的值域为（?∞，0]

12．函数f（x）是定义在R上的奇函数，当x＞0时，f(x)＝
x
1＋x
，则下列结论正确的是（　　）
A、f（x）在（?∞，0）上单调递减
B、关于x的不等式f（x）＋f（2x?1）＜0的解集为（?∞，
1
3
）
C、关于x的方程f(x)＝
1
3
x有三个实数解
D、?x1，x2∈R，|f（x2）?f（x1）|＜2

三、填空题：本大题共4小题，每小题5分，共20分．?


?

?
?
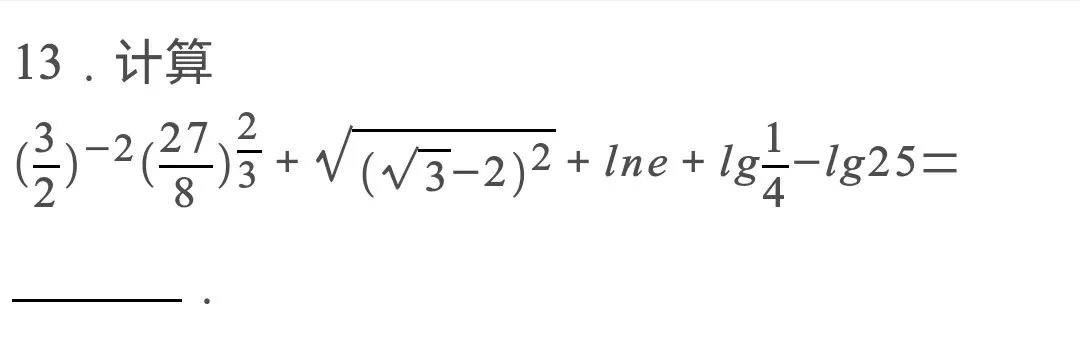四、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．设全集为R，A＝{x|x＜?1或x＞4}，B＝{x|1?a≤x≤2a＋3}．
（1）若a＝1，求A∩B，（?RA）∪B；
（2）已知A∩B＝?，求实数a的取值范围．
?

19．已知函数f（x）＝x2?（a＋1）x＋a．
（1）若a＝0，g（x）是定义在R上的奇函数，当x＜0时，g（x）＝f（x）．求g（x）的解析式；
（2）设实数a＜1，解关于x的不等式f（3x）＞0．?

?
22.?



相关文章
热门推荐
最新文章