2021年湖南高考数学答案解析
新高考Ⅰ卷数学答案解析
1.B
2.C
3.B
4.A
5.C
6.C
7.D
8.B
9.CD
10.AC
11.ACD
12.BD
13.a=1
14.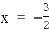
15.1
16.5;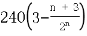
17.
(1)解:由题意得b1=a2=a1+1=2,b2=a4=a3+1=5
∵b1=a2=a1+1,∴a2-a1=1.
b2=a4=a3+1=a2+3 ∴a4-a2=3.
同理a6-a4=3
……
bn=a2n-a2n-2=3.
叠加可知a2n-a1=1+3(n-1)
∴a2n=3n-1
∴bn=3n-1.验证可得b1=a2=2,符合上式.
(2)解:∵a2n=a2n-1+1
∴a2n-1=a2n-1=3n-2.
∴设{an}前20项和为S20
∴S20=(a1+a3+…+a19)+(a2+a4+…+a20)
=145+155=300
18.
(1)解:
由题意得x=0,20,100.
P(x=0)=0.2
P(x=20)=0.8×0.4=0.32
P(x=100)=0.48
X | 0 | 20 | 100 |
P | 0.2 | 0.32 | 0.48 |
∴
(2)解:
小明先选择B,得分为y
∴y=0,80,100
P(y=0)=0.4
P(y=80)=0.6×0.2=0.12
P(y=100)= 0.6×0.8=0.48
y | 0 | 80 | 100 |
p | 0.4 | 0.12 | 0.48 |
∴
Ex=54.4 Ey=57.6
∴小明应先选择B.
19.
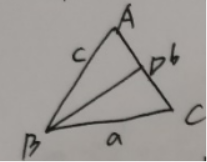
(1)由正弦定理
得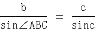 ,即
,即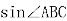 =
=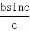
又由BD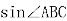 =asinc,得BD
=asinc,得BD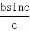 =asinc,
=asinc,
即 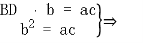 BD=b
BD=b
(2) 由AD=2DC,将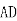 =2
=2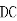 ,即
,即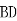 =
=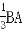 =
=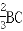
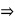 |
|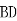 |2
|2 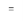
 |
|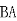 |2+
|2+  |
|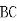 |2+
|2+ 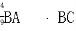
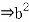 =
= c2+
c2+ a2+
a2+ c
c a
a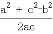
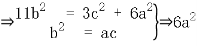 -11ac+3
-11ac+3 =0
=0
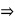 a=
a= c或a=
c或a= c
c
①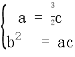
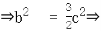 cos
cos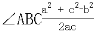 =
=
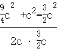 =
=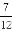
②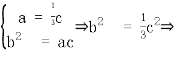 cos
cos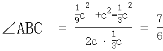 (x)
(x)
综上
cos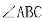 =
=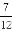
20.
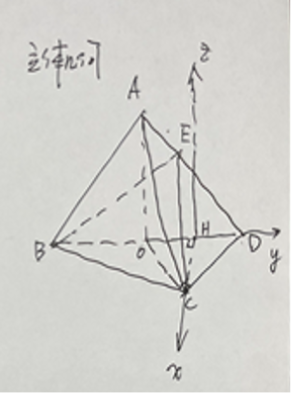
(1)证明:
由已知,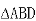 中AB=AD且O为BD中点
中AB=AD且O为BD中点
 AO⊥BD
AO⊥BD
又平面ABD⊥平面BCD
 AO⊥平面BCD且CD
AO⊥平面BCD且CD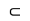 平面BCD
平面BCD
 AO⊥CD
AO⊥CD
(2)由于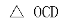 为正三角形,边长为1
为正三角形,边长为1
 OB=OD=OC=CD
OB=OD=OC=CD
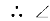 BCD=
BCD=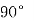
取OD中点H,连结CH,则CH⊥OD
以H为原点,HC,HD,HZ为x,y,z轴建立空间直角坐标系
由①可知,平面BCD的法向量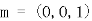
设C(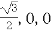 ),B(0,
),B(0,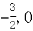 ),D(0,
),D(0,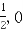 )
)
则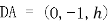
 DE=2EA
DE=2EA
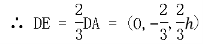
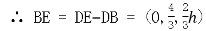 且
且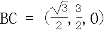
设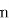 ⊥平面BEC
⊥平面BEC 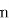 =(x,y,z)
=(x,y,z)
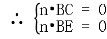 ,即
,即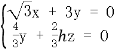
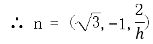
由于二面角E-BC-D为
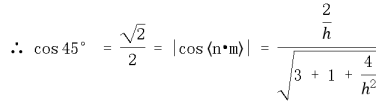
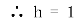
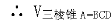 =
=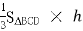 =
=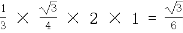
21.(1)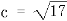 ,
, 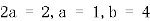
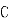 表示双曲线的右支方程:
表示双曲线的右支方程: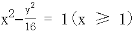
(2)设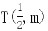 ,设直线AB的方程为
,设直线AB的方程为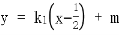 ,
,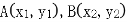
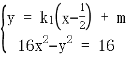 ,得
,得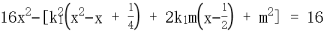
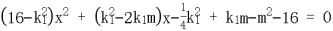
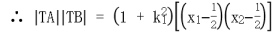

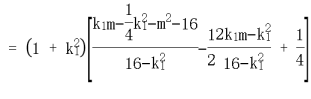
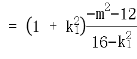
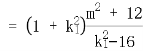
设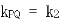 ,同理可得
,同理可得
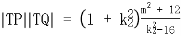
所以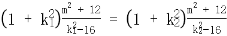
得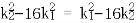
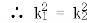
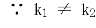
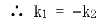
即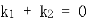
22.(1)f(x)=x-xlnx
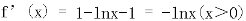
令f’(x)>0,则0<x<1,
令f’(x)<0,则x>1
∴f(x)的单调增区间为(0,1),单调减区间为(1,+∞).
(2)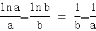
即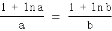 ,即f(
,即f( )=f(
)=f( )
)
令p= ,q=
,q= ,不妨设0<p<1<q,下面证明2<p+q<e.
,不妨设0<p<1<q,下面证明2<p+q<e.
① 先证p+q>2,当p≥2时结论显然成立.
当q∈(1,2)时,p+q>2,,则p>2-q,∴2-q<1.只需设f(p)>f(2-q).
即证当q∈(1,2)时,由f(p)>f(2-q)
令g(x)=f(x)-f(2-x).
g’(x)=f’(x)+f’(2-x)=-lnx-ln(2-x)=-ln[-(x-1)2+1]
当x∈(1,2)时,-(x-1)2+1<1,所以g’(x)>0,
∴g(x)在(1,2)上单调递增,
∴g(q)>g(1)=0,即f(q)>f(2-q)
②再设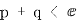 ,
,
当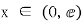 时,
时,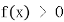 ,当
,当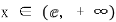 时,
时,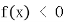
∴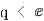
∵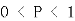 ∴
∴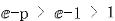
要证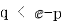 只需证
只需证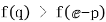
即证当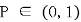 时,有
时,有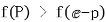
设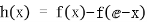 ,
,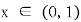 ,
,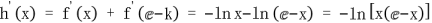
设 小于1的根为
小于1的根为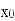 ,则
,则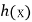 在
在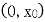 单调递增,在
单调递增,在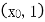 单调递减.
单调递减.

证毕



